以Bayesian來預測客戶的消費週期

本次的資料分析文章，讓我來介紹如何利用Bayesian分析，以解決現代店家普遍都會遇到的問題 - 那就是我的顧客何時會來？

這邊我們借用來自 Sharelike 會員集點專家 所提供的資料集。Sharelike享萊是一套電子集點系統， 目的是要解決「紙本集點卡」帶來的問題 - 顧客只需要到櫃檯的專屬平板上輸入手機號碼，用專屬印章「蓋章」之後，即可完成集點，省去攜帶與丟失紙本集點卡的困擾。

此外，因為有了手機資訊，店家便有機會與客戶保持聯繫，將相關優惠訊息以簡訊或推播等方式傳遞給客人，但問題是：要傳給哪些客戶？因為將訊息傳給錯誤的客人，除了效果不彰之外，也會被認為是無用的垃圾訊息，損害企業形象。

有了手機資訊，便能傳遞優惠訊息給客戶，但問題是：哪些客戶會對我的訊息有興趣？

理想的狀況是：根據過去的歷史資訊，若我們得知某客戶平均每三周會來消費一次，若兩周前他曾蒞臨，那麼我們可預期他下週很有可能再會來，因此在他蒞臨前，親手奉上最新專屬優惠，便是十分合理的作為。

然而，這在實務上並不容易做到，因為個別消費者往往資料稀少，難以精確估計出他們的消費週期。再者，除了知道他的週期之外，我們還會想知道這個週期估計的「精準程度」如何？ 因為這代表的是依據這個數字（消費週期）做出來的決策（寄送訊息給客戶）本身的決策風險有多高？

個別消費者往往資料過於稀少，難以精確估計他們的消費週期。

另外一種想法是：那我們就把大家的資料都拿來算一遍，就會得到大樣本的週期估計，而這樣總該精準了吧？確實是如此，但若群體平均週期是2.5天，難道每一位客戶都是每2.5天蒞臨嗎？這樣忽略掉個體差異的做法也不盡合理。

這種時刻就是Bayesian分析可以著力的地方：整合來自大群體樣本的精確度，以及個體小樣本的個體獨特性。

Bayesian分析整合來自群體大樣本的精確度，與個體小樣本的獨特性。

Bayes理論講述的是先驗機率(Prior probability)與後驗機率(Posterior probability)間的關聯，可以以一個概似函數(Likelihood function)做連接。

Posterior = Likelihood x Prior

一般的解釋是：Prior相當於「過去的經驗」，而Likelihood則是「新搜集到的知識」，最後整合出融合新舊經驗的Posterior。在這裡的例子，大群體的平均消費週期，構成了我們過去的經驗Prior，而依據手上對每一位消費者的資訊，可以得到對應的Likelihood，而我們的目標就是要求出整合兩者的Posterior

更正確一點來說：

「該消費者的週期」的分佈函數 = 依據個體資料做的分佈函數 x 大群體週期的分佈函數

接下來分析依下述的步驟進行：

1. 以「個體小樣本」去求得每個個人的消費週期 t 的機率分佈函數 T ~ f(t|λ)。其中λ代表的是我們對該個人所掌握的平均週期(所以是來自於小樣本)。
2. 再來我們將 λ 視為遵守某種機率分配的數字，用群體大樣本去「估計」他，企圖算出 λ ~ f(λ|.)。
3. 再將(1)(2)相乘，得到posterior  T’ ~  f(t|λ) x f(λ|.)，其意義為經群體大樣本校正後的個體週期估計
4. 最後利用得到的posterior去估算基本的統計量，像是平均數mean與變異數variance

為了能求得f(t|λ)，也就是單一客戶的個人週期分佈函數，我們從資料中選取一位蒞臨次數較多的客戶來獲取靈感。得到他的分佈狀況如下所示：

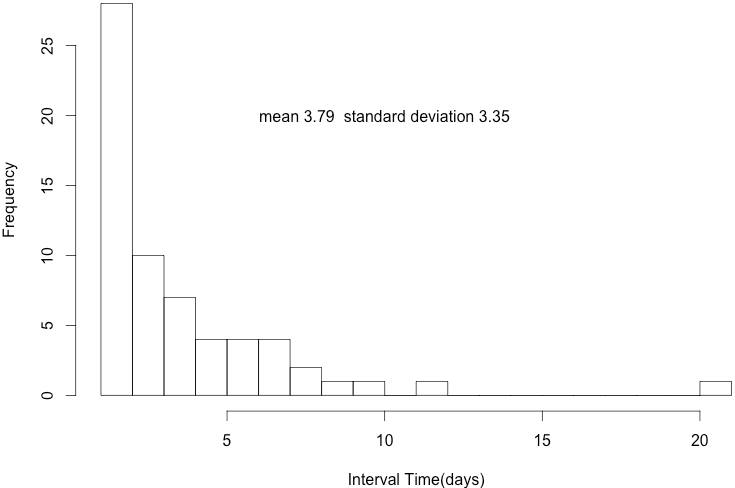
我們可以觀察到絕大多數的週期集中在1天，平均3.79天，整體呈現一個偏右分佈的狀況(skew to the right)，若我們以Exponential分佈去fit這個curve，可以得到以下的結果：

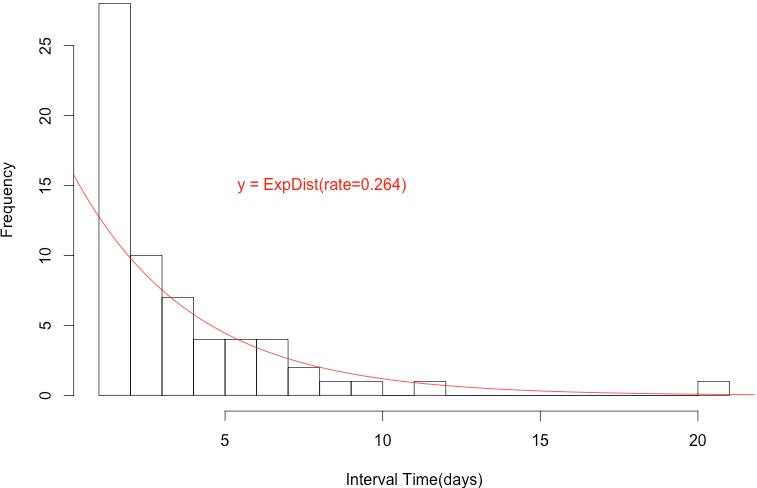
我們可以發現Exponential distribution大致上能解釋個體的週期分佈狀況，因此我們的Likelihood function便可以以底下的式子來建構：

P(t|λ) = ExpDist(t, λ=0.264)

然而僅以Exponential dist去fit個案的足跡資訊，缺點是當個案的資料量不足時，難以準確地描述個案的行為。

我們可以考慮用群體的資訊來做補充校正

我們把整個群體的資料倒進來，來建立Prior分配。若我們把整體消費者各自的平均週期算出來，然後對其分佈狀況作圖，可得到以下的結果：

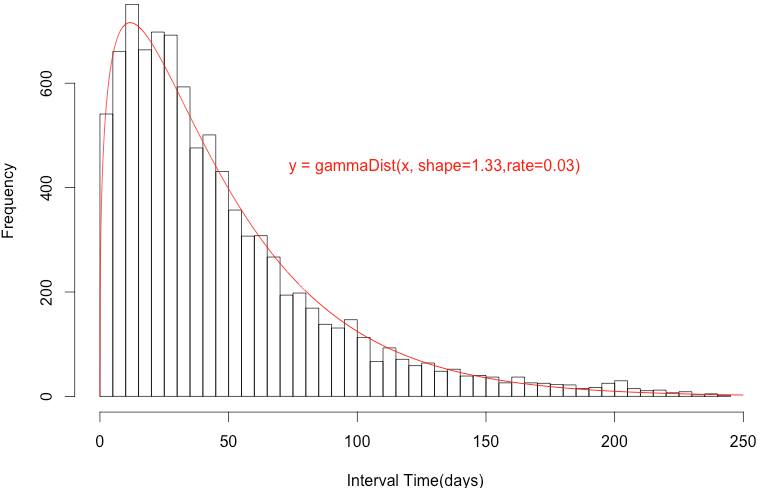
經過一些試誤後，發現Gamma distribution解釋整體的分佈狀況效果最好，因此Prior便可以底下的式子來建構：

P(λ|k,θ) = Gamma(λ|k=1.33, θ=0.03) 

整合上面的Prior與Likelihood便可得到我們的Posterior，也是一個 Gamma 分佈。

Gamma(t|k',θ') = ExpDist(t|λ) * Gamma(λ|k=1.33,θ=0.03)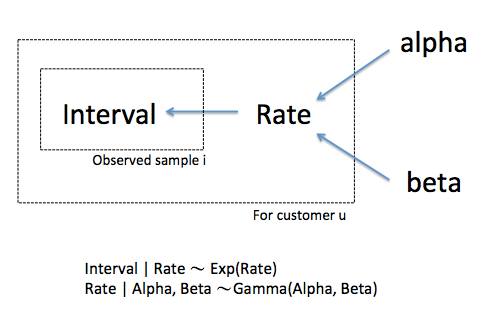 

使用上，只要我們知道Posterior的參數 k',θ' ，即可得知任何時間t之下，該使用者出現的機率。欲得知k',θ' ，可以善用樣本資料與Prior分佈參數k,θ之間的關係 :

k' = k + n
1/θ' = 1/θ + nx̅

因此，我們要先估計Prior分佈的θ, k，本文採用數值方法Markov Chain Monte Carlo方法裡的Metropolis-Hastings演算法(MH)。MH演算法提供了一個簡便的方式，可對困難的機率分佈函數進行抽樣，來「模擬」其分佈函數實際的情形。

讓我們來實際探究我們的模型：假設一位客人A，以目前搜集到的10筆週期數據 = {12,2,13,2,34, ...}，其樣本的平均週期是18天。我們把用這樣的小樣本做一個分佈圖，拿來跟Posterior分佈作圖，可以看出經過Prior校正前後的變化：

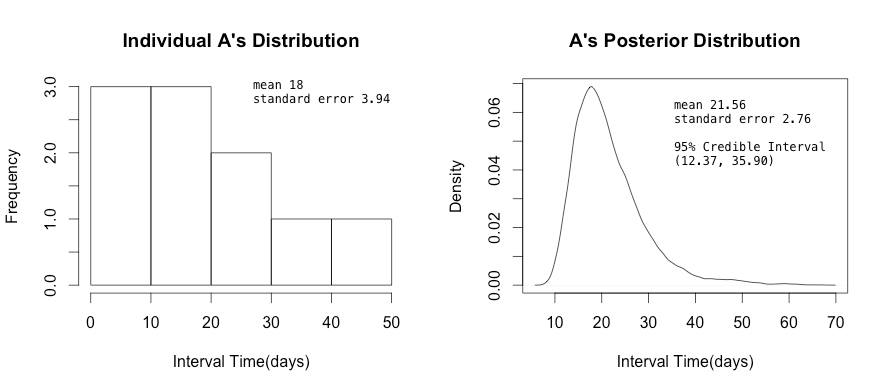
若我們找另外一位客戶B，其數據量較大，有56筆 ={1,2,3,1,6,5,2,2,3,5,7,2,1, ...} ，樣本的平均週期是4.32天。我們把用這樣的樣本做分佈圖，拿來跟Posterior分佈作圖，可以看出經過Prior校正前後的變化：

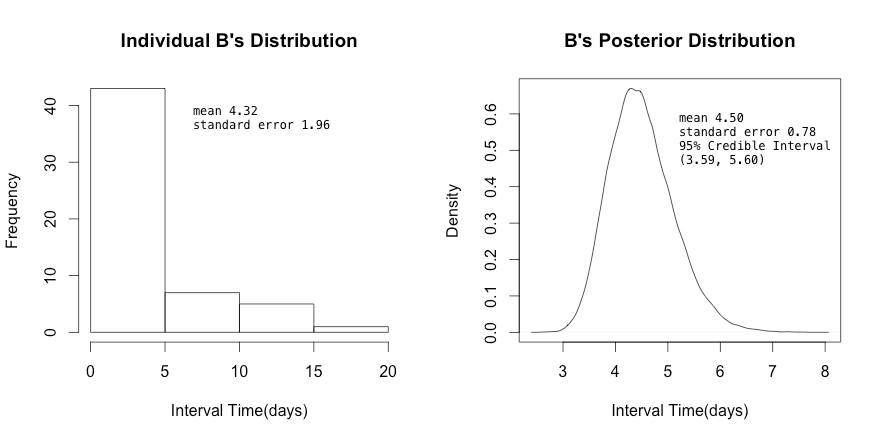
隨著客戶累積的資料量增加，我們對其行為越來越有把握，Bayesian Posterior的估計值也會自動隨之調整。

若將上述的方法對每一位客戶做運算，則可以得到他們每個人合理的消費週期。更重要的是，還可以得知這樣的估計，其誤差程度有多少 - 店家便能依此去篩選適當對象，只針對一定風險程度以下的客戶進行促銷活動，借此提高成功率，降低經營風險。

接著我們就會好奇：用Posterior做出來的估計，放在真實世界的表現如何？

這邊我們設計一個實驗：透過計算training set中有出現過的客戶，他們最近一次的消費時間(Recency)以及我們對他的消費週期的95%貝氏可靠區間(95% Credible Interval)，我們建構以下的預測模式：

下次該客戶出現的時間範圍 = 最近一次出現的時間 +/- 該客戶95% CI的上下界

有別於前面用來建構模型的訓練樣本(training set)，我們另外取得一組樣本來作為測試樣本(test set)，並以前述的預測模式，以下述的步驟來做預測：

1. 對所有training set裡有出現的客戶，計算每位客戶「下次應該出現的時間範圍」
2. 我們篩選出按照training set所做的預測，理應要在與test set相同取樣的時間裡(eg. 2015-11-01 到 2015-11-30) 出現的客戶的清單
3. 將(2)所得的清單，拿來跟實際test set裡，該客戶真正出現的時間作比較 ，若在預期的時間內出現則視為「成功」，反之則視為「失敗」
4. 算出預測模式的 Sensitivity(該出現而有出現)、Specificity(不該出現而沒有出現)，以及整體Accuracy

符合上述條件的個案共有7728位，其中被預期要出現但實際上沒有出現的，共有2677 (False Positive)，沒有被預期要出現的但卻出現的，共有663位(False Negative)，整體的Sensitivity約57.1%、Specficity 56.7%、Accuracy 56.8%

上述的結果乍看並不理想。但實務上，店家對於風險較高的客人，本來就不會預期他會按時來消費，因此若將這樣的客人事先予以排除，實現「風險管控」的作為，我們的預測模式便會是：

下次該客戶出現的時間範圍 = 最近一次出現的時間 +/- 該客戶95% CI的上下界

這邊以14天作為cutoff純粹是一個經營上的考量，依照店家營運的需求而訂。以上述的模式進行預測，符合條件的個案共有3656位，其中被預期要出現但實際上沒有出現的，共有24 (False Positive)，沒有被預期要出現的但卻出現的，共有39位(False Negative)，整體的Sensitivity約98.9%、Specficity 70.4%、Accuracy 98.3%

若對週期估計誤差小於14天內的客戶，預測未來是否會按期消費？模型準確度可達98.3%

那至於誤差大於14天以上的客戶怎麼辦？目前只能說我們對他們這個群體還不夠理解，還有許多研究要做。